Solving Gear Questions on the Mechanical Aptitude Test
By following this detailed lesson outline, you will gain a strong understanding of gears and gear systems, as well as the skills necessary to solve gear-related questions on the mechanical aptitude test.
Quick Navigation
Click to Expand
Introduction to Gears
Looking for prep material on this topic?
Practicing is a proven way to score higher on your Mechanical Aptitude Test. Find full prep packages to ace your assessment!
Definition and purpose of gears
Gears are mechanical components with teeth that mesh with other gears to transmit rotational motion, force, or torque. They are used in various machines and mechanisms to:
- Change the speed of rotation: Gears can increase or decrease the rotational speed of an output shaft compared to an input shaft.
- Change the direction of rotation: Gears can reverse the direction of rotation.
- Transfer motion between non-parallel shafts: Some types of gears can transmit motion between shafts that are not parallel.
- Increase or decrease torque: Gears can amplify or reduce the torque, providing a mechanical advantage or disadvantage.
Different types of gears
Spur gears
Helical gears have teeth that are cut at an angle to the gear's axis of rotation. The angled teeth engage gradually, resulting in smoother and quieter operation compared to spur gears. Like spur gears, helical gears transmit motion between parallel shafts but with improved efficiency and reduced noise.
Bevel gears
Bevel gears have conical shapes and are used to transmit motion between intersecting shafts, typically at a 90-degree angle. The teeth can be straight, spiral, or hypoid, with each type offering different performance characteristics. Bevel gears can change the speed, torque, and direction of rotation between non-parallel shafts.
Worm gears
Worm gears are a special type of gear used to transmit motion between non-parallel and non-intersecting shafts. A worm gear consists of a screw-like gear (the worm) that meshes with a larger gear (the worm wheel). Worm gear assemblies provide a high reduction ratio and can achieve a large mechanical advantage, but they usually operate with lower efficiency due to friction.
Basic gear terminology
- Gear teeth: The protrusions on a gear's circumference that interlock with the teeth of another gear, allowing them to transmit motion. The shape and size of gear teeth can vary depending on the type of gear and the application.
- Pitch: The pitch of a gear refers to the distance between corresponding points on adjacent teeth, typically measured along the pitch circle (an imaginary circle that passes through the center of the gear teeth). The pitch determines how well gears mesh together and directly affects the gear ratio.
- Diameter: The diameter of a gear is the distance across the gear, usually measured at the pitch circle. Larger gears typically have more teeth and provide more torque, while smaller gears have fewer teeth and deliver higher rotational speed.
- Gear ratio: The gear ratio is the relationship between the number of teeth on two meshing gears. It is calculated by dividing the number of teeth on the output gear (the driven gear) by the number of teeth on the input gear (the driver gear). The gear ratio determines the mechanical advantage, speed, and torque of a gear system. A high gear ratio provides greater torque at lower speeds, while a low gear ratio provides higher speed at lower torque.
Gear Ratios and Mechanical Advantage
Looking for prep material on this topic?
Practicing is a proven way to score higher on your Mechanical Aptitude Test. Find full prep packages to ace your assessment!
Understanding gear ratios
Definition and purpose
Gear ratio is the relationship between the number of teeth on two meshing gears. It determines how the speed and torque are transferred between the gears, allowing for various mechanical advantages. Gear ratios are essential in designing gear systems for specific applications, as they can be used to control the output speed and torque, based on the input speed and torque.
Calculating gear ratios
To calculate the gear ratio between two meshing gears, divide the number of teeth on the output gear (the driven gear) by the number of teeth on the input gear (the driver gear). The formula is:
Gear Ratio = (Number of Teeth on Driven Gear) / (Number of Teeth on Driver Gear)
For example, if the driven gear has 40 teeth and the driver gear has 10 teeth, the gear ratio is 40/10 = 4. This means that the driven gear will rotate one-fourth as fast as the driver gear, but with four times the torque.
Mechanical advantage
Definition and importance
Mechanical advantage is the ratio of output force (or torque) to input force (or torque) in a mechanical system. In gear systems, the mechanical advantage is equal to the gear ratio. A higher mechanical advantage means that a system can amplify the input force or torque, making it easier to perform tasks that require significant force or torque. Mechanical advantage is crucial in the design of machines and mechanisms, as it allows engineers to optimize the system for a specific purpose or application.
Examples of mechanical advantage in gear systems
A bicycle's gears
In a bicycle, the gear system enables the rider to adjust the mechanical advantage by changing the gear ratio. A lower gear ratio (smaller front chainring and larger rear sprocket) provides a higher mechanical advantage, making it easier to pedal uphill or start from a stop. A higher gear ratio (larger front chainring and smaller rear sprocket) provides a lower mechanical advantage, allowing the rider to achieve higher speeds on flat surfaces or downhill.
A car's transmission
In a car, the transmission uses different gear ratios to provide the engine with a range of mechanical advantages. Lower gear ratios provide higher mechanical advantage, which helps the car accelerate or climb steep hills. Higher gear ratios provide lower mechanical advantage, allowing the car to maintain high speeds with lower engine RPMs, improving fuel efficiency.
Speed, torque, and power relationships
Speed and torque trade-offs
In a gear system, there is a trade-off between speed and torque. When the gear ratio is increased (by using a larger driven gear or smaller driver gear), the output speed decreases while the output torque increases. Conversely, when the gear ratio is decreased (by using a smaller driven gear or larger driver gear), the output speed increases while the output torque decreases. This trade-off allows engineers to design gear systems that meet specific speed and torque requirements for various applications.
Conservation of power in gear systems
The conservation of power principle states that the power input to a gear system is equal to the power output, assuming no energy losses due to friction or other factors. Power is the product of torque and rotational speed. In gear systems, the input power (Pin) equals the output power (Pout):
Pin = Pout
Input Torque (Tin) × Input Speed (ωin) = Output Torque (Tout) × Output Speed (ωout)
This relationship shows that while the speed and torque can be manipulated using gear ratios, the overall power remains constant (assuming no energy losses). This principle is crucial in understanding how gear systems can be designed to meet specific power requirements while manipulating speed and torque.
For example, if a gear system is designed to increase torque, the output speed will decrease to maintain the same power level. Conversely, if the gear system is designed to increase speed, the output torque will decrease to keep the power constant.
Understanding the conservation of power principle, along with the concepts of gear ratios and mechanical advantage, will help you analyze and solve various gear-related problems in mechanical aptitude tests and real-life applications.
Gear Trains
Looking for prep material on this topic?
Practicing is a proven way to score higher on your Mechanical Aptitude Test. Find full prep packages to ace your assessment!
Types of gear trains
Gear trains are combinations of two or more gears used to transmit motion, force, or torque from one shaft to another. They are commonly used in various machines and mechanisms to achieve specific speed, torque, and direction requirements. There are three main types of gear trains:
Simple gear trains
A simple gear train consists of two or more gears mounted on parallel shafts that mesh directly with each other. The input gear (driver) transmits motion to the output gear (driven) through intermediate gears, if present. Simple gear trains are used to change the speed, torque, and direction of rotation between the input and output shafts.
Compound gear trains
A compound gear train consists of two or more gears mounted on the same shaft, with each pair of gears meshing with another pair on a different shaft. Compound gear trains allow for larger gear ratios than simple gear trains, making them suitable for applications requiring significant speed reductions or torque increases. They can also be more compact and efficient compared to simple gear trains with the same gear ratio.
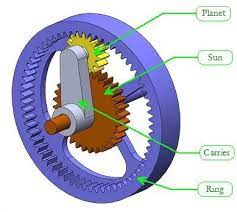
Epicyclic (planetary) gear trains
Epicyclic or planetary gear trains consist of a central gear (sun gear) that meshes with one or more gears (planet gears) rotating around it. The planet gears are mounted on a carrier, which itself can rotate, and they also mesh with an outer gear (ring gear) that encircles the entire assembly. Planetary gear trains are used in applications requiring high gear ratios, compact size, or multiple output shafts with different speeds and torques.
Calculating gear ratios in gear trains
Simple gear trains
To calculate the overall gear ratio of a simple gear train, divide the number of teeth on the output gear (driven gear) by the number of teeth on the input gear (driver gear). If there are intermediate gears in the gear train, multiply the gear ratios of each gear pair:
Overall Gear Ratio = (Teeth on Driven Gear 1 / Teeth on Driver Gear 1) × (Teeth on Driven Gear 2 / Teeth on Driver Gear 2) × ...
Compound gear trains
To calculate the overall gear ratio of a compound gear train, find the gear ratio of each pair of meshing gears and then multiply the gear ratios together:
Overall Gear Ratio = (Teeth on Driven Gear 1 / Teeth on Driver Gear 1) × (Teeth on Driven Gear 2 / Teeth on Driver Gear 2) × ...
Note that gears mounted on the same shaft have the same rotational speed, so their gear ratio does not affect the overall gear ratio of the compound gear train.
Epicyclic gear trains
Calculating gear ratios in epicyclic gear trains can be more complex due to the multiple moving components. One common method is to use the tabular method, which involves fixing one component (sun gear, planet carrier, or ring gear) and treating the other two components as input and output. The gear ratio can then be calculated based on the number of teeth on each component and the fixed component's relationship with the others:
Overall Gear Ratio = (Teeth on Fixed Component ± Teeth on Input Component) / Teeth on Output Component
The choice between addition and subtraction depends on the relative direction of rotation of the input and output components when the fixed component is held stationary. If the input and output components rotate in the same direction, use subtraction; if they rotate in opposite directions, use addition. It's important to note that the overall gear ratio can change depending on which component is fixed, so it's necessary to specify the fixed component when calculating the gear ratio in an epicyclic gear train.
For example, consider a planetary gear train with a sun gear having 20 teeth, planet gears having 30 teeth each, and a ring gear having 80 teeth. To calculate the gear ratio when the planet carrier is fixed (input is the sun gear, and output is the ring gear):
Overall Gear Ratio = (Teeth on Fixed Component + Teeth on Input Component) / Teeth on Output Component = (30 + 20) / 80 = 50 / 80 = 5 / 8
In this example, the overall gear ratio is 5:8 when the planet carrier is fixed.
By understanding the types of gear trains and how to calculate gear ratios for each type, you can analyze and solve various gear-related problems in mechanical aptitude tests and real-life applications. By mastering these concepts, you'll be better equipped to tackle gear questions and design efficient gear systems for specific requirements.
Solving Mechanical Aptitude Test Gear Questions
Looking for prep material on this topic?
Practicing is a proven way to score higher on your Mechanical Aptitude Test. Find full prep packages to ace your assessment!
Identifying the type of gear question
Gear questions in mechanical aptitude tests can be categorized into four main types:
Basic gear ratios: These questions involve calculating gear ratios for simple gear pairs or gear trains. They test your understanding of gear ratios and how they affect speed and torque.
Gear trains: These questions require you to analyze and calculate gear ratios for more complex gear systems, such as compound and epicyclic gear trains. Familiarize yourself with different types of gear trains and their properties to tackle these questions effectively.
Direction of rotation: Direction of rotation questions test your ability to determine the direction in which gears will rotate based on the arrangement and direction of the driving gear. Understanding the basics of how gears interact with each other is essential for answering these questions.
Speed and torque relationships: These questions involve analyzing the relationships between speed, torque, and power in gear systems. They require an understanding of mechanical advantage and the conservation of power principle.
Strategies for solving gear questions
2) Breaking down complex problems into simpler parts
For more complex gear problems, break the problem down into smaller parts. Analyze each part separately and then combine the results to solve the overall problem.
3) Using gear ratios and mechanical advantage concepts
Leverage your understanding of gear ratios, mechanical advantage, and the conservation of power principle to tackle gear questions effectively. Remember the formulas and relationships between speed, torque, and power when solving problems.
By understanding the different types of gear questions, employing problem-solving strategies, and practicing various problems, you can improve your ability to solve gear questions in mechanical aptitude tests. The key is to familiarize yourself with gear concepts and principles, visualize gear systems, and break down complex problems into simpler parts. With practice and determination, you can excel at gear-related questions and boost your mechanical aptitude test performance.
Free Sample Mechanical Aptitude Test Gear Question Quiz
Looking for prep material on this topic?
Practicing is a proven way to score higher on your Mechanical Aptitude Test. Find full prep packages to ace your assessment!